# 세줄 요약 #
- We present a residual learning framework to ease the training of networks that are substantially deeper than those used previously.
- We provide comprehensive empirical evidence showing that these residual networks are easier to optimize, and can gain accuracy from considerably increased depth (evaluate residual nets with a depth of up to 152 layers).
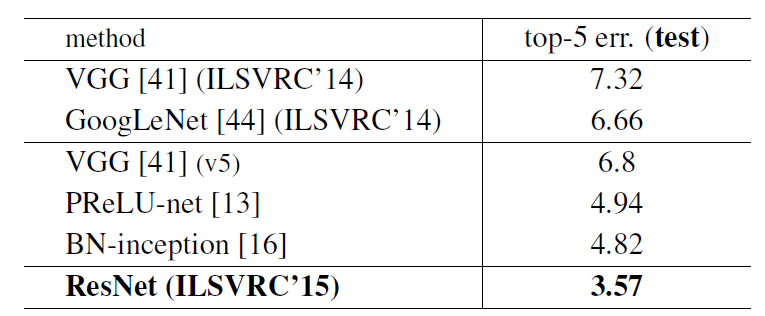
- This result won the 1st place on the ILSVRC 2015 classification task (3.57% error on the ImageNet test set).
# 상세 리뷰 #
1. Introduction
- Is learning better networks as easy as stacking more layers?
- An obstacle to answering this question was the notorious problem of vanishing/exploding gradients.
- When deeper networks are able to start converging, a degradation problem has been exposed.
- with the network depth increasing, accuracy gets saturated.
- adding more layers to a suitably deep model leads to higher training error.

- We address the degradation problem by introducing a deep residual learning framework.
- There exists a solution by construction to the deeper model: the added layers are identity mapping
- Instead of hoping each few stacked layers directly fit a desired underlying mapping, we explicitly let these layers fit a residual fitting
- The formulation of F(x) + x can be realized by feedforward neural networks with "shortcut connection"

- We present comprehensive experiments on ImageNet to show the degradation problem and evaluate our method.
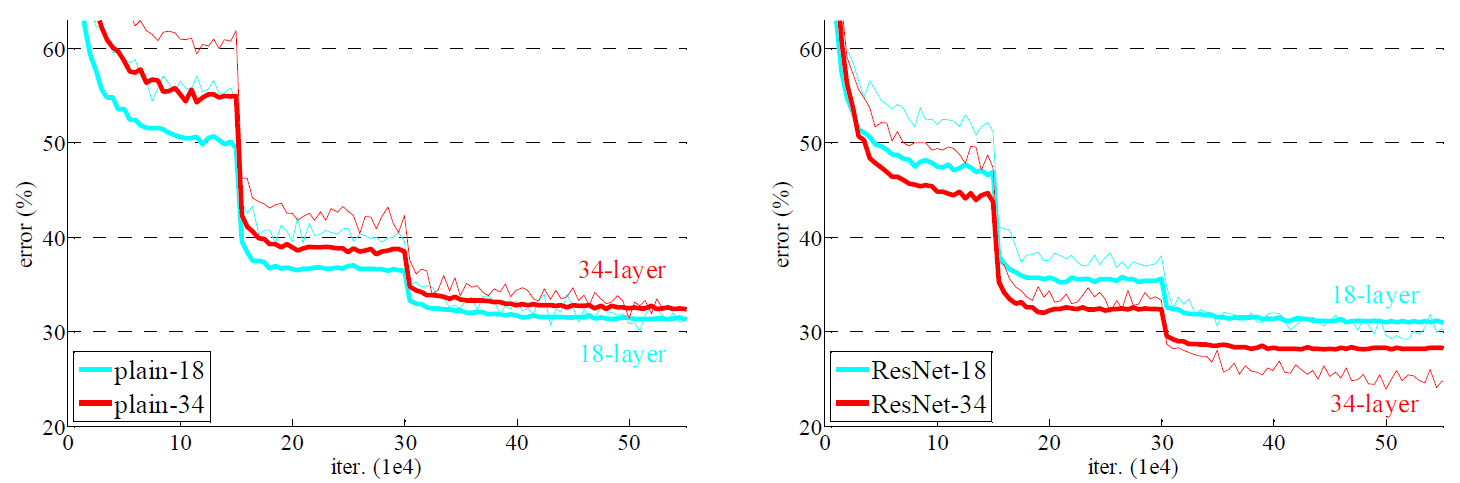
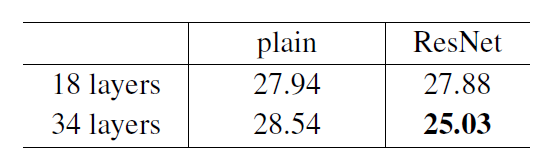
- 1) Our extremely deep residual nets are easy to optimize.
- 2) Our deep residual nets can easily enjoy accuracy gains from greatly increased depth.
- Our ensemble has 3.57% top-5 error on the ImageNet test set, and won the 1st place in the ILSVRC 2015 classification competition.
2. Deep Residual Learning
- Residual Learning
- H(x): An underlying mapping to be fit by a few stacked layers
- x: The inputs to the first of these layers.
- H(x) - x: hypothesis 'H(x) & x' can asymptotically approximate the residual functions.
- (assuming that the input and output are of the same dimensions)
- F(x) = H(x) -x: we explicitly let these layers approximate a residual function.
- F(x) + x: The original mapping.
- Identity Mapping by Shortcuts
- We adopt residual learning to every few stacked layers.
- A building block:
- y = F(x, {Wi}) + x (eq1)
- If dimensions of x and F are not equal, we can perform a linear projection Ws (= matching dimension).
- y = F(x, {Wi}) + Ws * x (eq2)

- Network Architectures

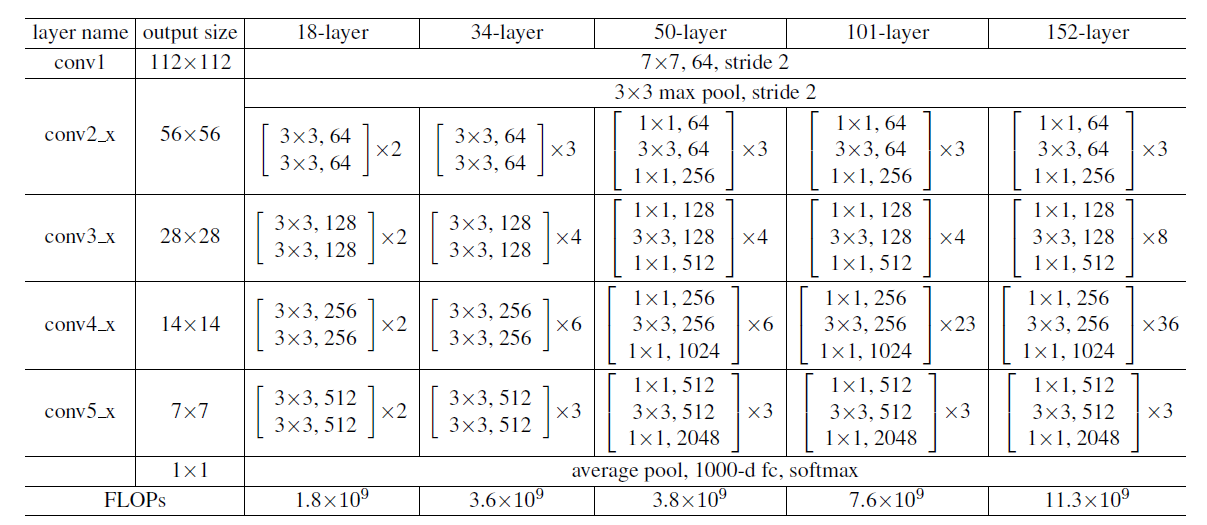
3. Experiments
- ImageNet classification.
* Reference: He, Kaiming, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
728x90
728x90




댓글